
16. Schwingungen
1. Zwei Sinusfunktionen werden addiert. Ist die Summenfunktion wieder eine Sinusfunktion? Wenn ja, welches ist ihre Frequenz? Antworte für die untenstehenden Fälle (a), (b), (c) und (d).
Die beiden Ausgangsfunktionen haben
(a) gleiche Amplituden, gleiche Kreisfrequenzen und gleiche Anfangsphasen;
(b) verschiedene Amplituden, gleiche Kreisfrequenzen, gleiche Anfangsphasen;
(c) verschiedene Amplituden, gleiche Kreisfrequenzen, verschiedene Anfangsphasen;
(d) gleiche Amplituden, verschiedene Frequenzen, gleiche Anfangsphase.
Lösung:
(a) Summenfunktion ist Sinusfunktion; Frequenz ist dieselbe wie die der Summanden;
(b) Summenfunktion ist Sinusfunktion; Frequenz ist dieselbe wie die der Summanden;
(c) Summenfunktion ist Sinusfunktion; Frequenz ist dieselbe wie die der Summanden;
(d) Summenfunktion ist keine Sinusfunktion.
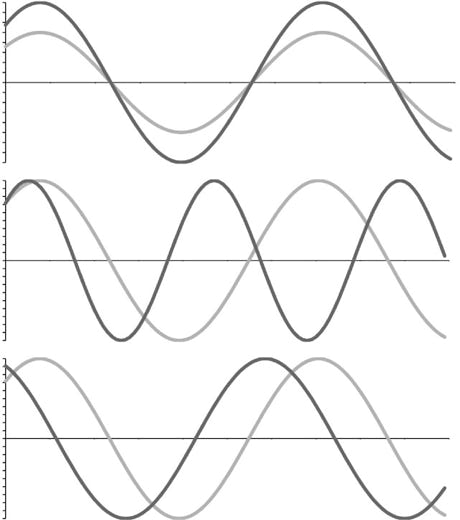
2. In den Diagrammen der Abbildung ist der Ort eines schwingenden Körpers als Funktion der Zeit dargestellt, und zwar in jedem der drei Teilbilder für zwei Schwingungen. Vergleiche die beiden Schwingungen für jedes der Teilbilder nach dem Muster:
„Die beiden Schwingen haben dieselbe Amplitude, aber verschiedene Frequenzen und verschiedene Anfangsphasen“, etc.
Lösung:
oben: verschiedene Amplituden, gleiche Frequenz, gleiche Anfangsphase;
Mitte: gleiche Amplitude, verschiedene Frequenzen, gleiche Anfangsphase;
unten: gleiche Amplitude, gleiche Frequenz, verschiedene Anfangsphasen.
3. Eine periodische Funktion wird in Sinusfunktionen zerlegt. Was kann man über ihr Spektrum sagen?
4. Wovon hängt die Periodendauer eines Federschwingers ab? Wie ist der quantitative Zusammenhang?
5. Wovon hängt die Periodendauer eines Fadenpendels ab? Wie ist der quantitative Zusammenhang?
6. Die Periodendauer eines Pendels soll verdoppelt werden. Was ist zu tun?
7. Warum hängt die Periodendauer eines Pendels nicht von der Masse ab?
8. Beschreibe in Worten (evtl. auch mit einer Skizze), die Impuls- und die Energiebilanz eines Pendels.
9. Beschreibe in Worten (evtl. auch mit einer Skizze), die Ladungs- und die Energiebilanz des Schwingkreises.
10. Wie müssen die Bauelemente des Schwingkreises beschaffen sein, damit die Periodendauer groß wird?
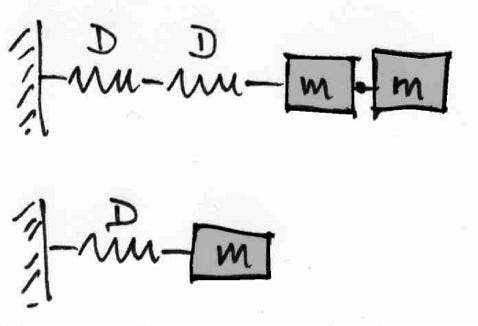
11. Vergleiche die Schwinger in der Abbildung. Der eine schwingt schneller als der andere. Welches ist der schnellere? Um wie viel ist er schneller?
Lösung:
Der untere schwingt doppelt so schnell wie der obere.
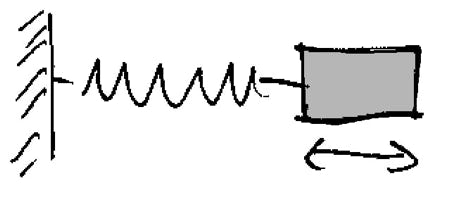
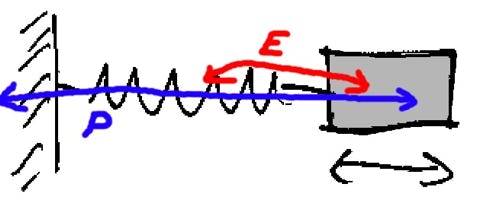
12. Beschreibe den Weg von Impuls und Energie, wenn der Körper Schwingungen ausführt. Prüfe dabei, ob die Flussrichtung des Impulses in der Feder stimmt.
Lösung:
Wenn der Körper im rechten Umkehrpunkt ist, ist die Feder gespannt: Impuls fließt nach links, d.h. aus dem Körper heraus. Dessen Impuls wird dabei negativ – wie es zu erwarten war.
13.
(a) Wie viele verschiedene Eigenschwingungen kann das abgebildete System ausführen?
(b) Jemand hat das System irgendwie in Bewegung versetzt. Woran erkennt man, ob es eine Eigenschwingung ausführt?
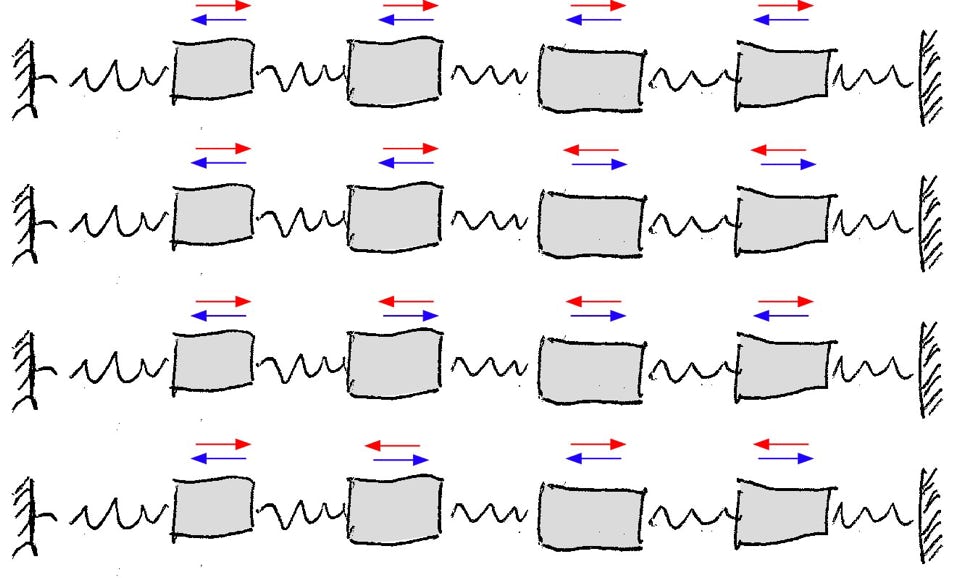
(c) Skizziere durch Pfeile in der Abbildung so viele Eigenschwingungen wie möglich. Falls der Platz nicht reicht, mach eine neue Abbildung.
Lösung:
(a) Vier
(b) Es führt eine Eigenschwingung aus, wenn sich jeder der vier Körper sinusförmig bewegt.
(c)
14. Beschreibe zwei Verfahren der Bestimmung der Federkonstante einer Feder.
Lösung:
– Man hängt einen Körper bekannter Masse m an die Feder, misst die Auslenkung und dividiert Impulsstrom m · g durch die Auslenkung;
– man hängt einen Körper bekannter Masse m an die Feder und lässt das System schwingen; aus Schwingungsdauer und Masse berechnet man die Federkonstante.
15. Jemand hat eine Pendeluhr mit auf den Mond genommen. Funktioniert dort die Uhr? Begründe.
Lösung:
Da auf dem Mond die Gravitationsfeldstärke kleiner ist als auf der Erde, schwingt das Pendel langsamer. Man brauchte also eine andereZahnradübersetzung für die Zeiger der Uhr.
Die Uhr geht zunächst auch deshalb nicht, weil das „Gewicht“ zu wenig Energie liefert. Der Energievorrat für die aufgezogene Uhr m · g · h ist proportional zur Feldstärke g. Man müsste also ein schwereres Gewicht verwenden.
16. Ein Astronaut eines fernen Planetensystems besucht uns. Er bringt ein Fadenpendel der Länge
l = 150 cm mit und berichtet, dass dieses Pendel auf seinem Heimatplaneten genau 45 volle Schwingungen in einer Minute macht.
(a) Wie groß ist der Ortsfaktor (die Gavitationsfeldstärke) auf dem Planeten des Astronauten?
(b) Wie viele Schwingungen macht dieses Pendel in einer Minute auf der Erde?
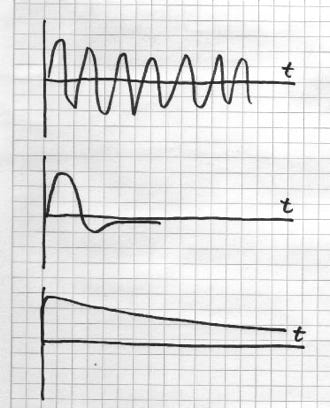
17. In einem Ziegermessinstrument befindet sich ein Dämpfer. Wie muß die Dämpfung gewählt werden? Warum?
Lösung:
Ohne Dämpfung würde der Zeigen lange um seine endgültige Stellung herumpendeln (oberes Bild). Wählt man die Dämpfung zu groß, so braucht der Zeiger (ohne zu pendeln) lange, bis er den Endwert erreicht (unteres Bild). Es gibt also eine optimale Dämpfung, für die die endgültige Zeigerstellung am schnellsten erreicht wird (mittleres Bild).
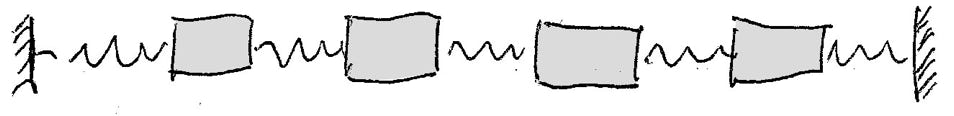

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Aliquam tincidunt lorem enim, eget fringilla