





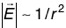


15. Das elektrische und das magnetische Feld, Induktion
15.2 Der Kondensator
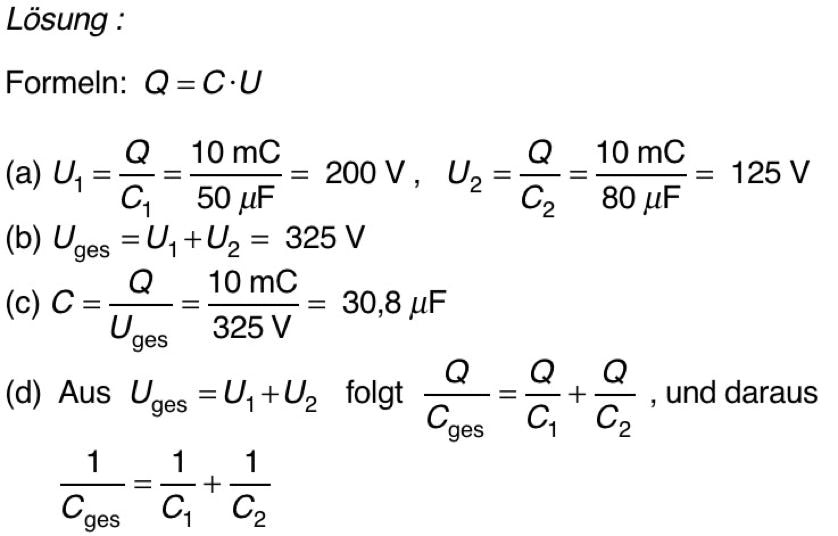
1. Zwei Kondensatoren mit den Kapazitäten C1 = 50 μF und C2 = 80 μF werden hintereinander geschaltet und mit der Ladung Q = 10 mC aufgeladen.
(a) Wie groß ist die Spannung U1 von Kondensator 1 und die Spannung U2 von Kondensator 2?
(b) Wie groß ist die Gesamtspannung Uges der Kondensatoren?
(c) Wie groß ist die Kapazität der gesamten Anordnung Cges?
(d) Formuliere eine Regel für die Gesamtkapazität bei der Reihenschaltung von Kondensatoren.
2. Zwei Kondensatoren werden parallel geschaltet. Leite eine Regel für die Gesamtkapazität bei der Parallelschaltung von Kondensatoren her.
3. Ein Plattenkondensator mit Plattenfläche A = 40 cm2 und Plattenabstand d = 4 mm wird mit der Ladung Q = 20 μC geladen.
(a) Wie groß ist die Spannung U des Kondensators, seine Kapazität C und der Betrag der Feldstärke E im Innern des Kondensators?
(b) Die Platten werden von d auf den doppelten Abstand 2d auseinander gezogen. Wie ändern sich die Ladung Q, die Spannung U, die Kapazität C und der Feldstärkebetrag E?
Hinweis: Bei Aufgabenteil (b) reicht die Angabe, ob die Werte im Vergleich zu ( a) gleich bleiben, sich verdoppeln oder halbieren. Exakte Zahlenwerte sind nicht nötig. (ε0 = 8,854 · 10-12 C/(Vm))
4. Die Platten eines geladenen Kondensators werden auf den doppelten Abstand gebracht.
(a) Die Ladung auf den Platten wird dabei konstant gehalten. Was passiert dabei mit der Kapazität, der Spannung und der elektrischen Feldstärke?
(b) Die Spannung wird konstant gehalten. Was passiert dabei mit der Kapazität, der Ladung und der elektrischen Feldstärke?
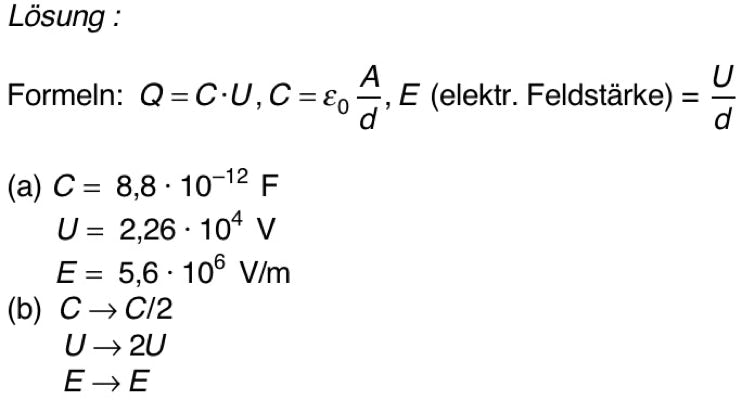
Lösung:
(a) Kapazität: nimmt auf die Hälfte ab; Spannung: wächst auf das Doppelte an; elektrische Feldstärke: bleibt gleich
(b) Kapazität: nimmt auf die Hälfte ab; Ladung: nimmt auf die Hälfte ab; elektrische Feldstärke: nimmt auf die Hälfte ab
5. Von welchen Größen hängt die in einem Kondensator gespeicherte Energie ab? Wie lautet der quantitative Zusammenhang? Mit welchen Überlegungen kannst du die Formel wiederfinden, wenn du sie vergessen hast?
Lösung:
Die Energie hängt von der Spannung und der Kapazität ab (bzw. von der Ladung und der Kapazität).
Die Gleichung ist analog zu der für die kinetische Energie. Die Masse ist ein Maß dafür, wie viel Impuls ein Körper bei gegebener Geschwindigkeit hat. Entsprechend ist die Kapazität ein Maß dafür, wie viel elektrische Ladung ein Kondensator bei gegebener Spannung hat. Eine Geschwindigkeitsdifferenz ist ein Antrieb für einen Impulsstrom. Entsprechend ist eine elektrische Potenzialdifferenz ein Antrieb für einen elektrischen Strom.
Die Spannung steht in der Gleichung im Quadrat. So ist die Energie unabhängig vom Vorzeichen der Spannung (so wie die kinetische Energie unabhängig vom Vorzeichen der Geschwindigkeit ist).
7. Ein Plattenkondensator wird mit 1000 Volt aufgeladen. Das dabei verwendete Hochspannungsnetzgerät kann auf höchstens 1000 Volt eingestellt werden.
(a) Welches Experiment kann man machen um den Feldstoff zwischen den Platten nach dem Laden zu vermehren?
(b) Was lässt sich über die Energiedichte des Feldes zwischen den Platten bei diesem Experiment sagen?
Lösung:
(a)Man trennt den Kondensator vom Netzgerät und vergrößert den Plattenabstand. Dabei bleiben Ladung und Feldstärke konstant. Mit zunehmendem Volumen des felderfüllten Raums nimmt daher auch die Menge des Feldstoffs zu.
(b) Da die Feldstärke konstant bleibt, bleibt auch die Energiedichte (proportional zur Feldstärke) konstant.
8. Zwischen den Anschlüssen eines Kondensators, dessen Kapazität C =1 F beträgt, wird eine Spannung von 5 Volt gemessen. Der Kondensator wird über einen Widerstand entladen. Berechne die dabei erzeugte Entropie. (Falls dir der Wert irgendeiner Größe fehlt, mach eine vernünftige Annahme darüber.)
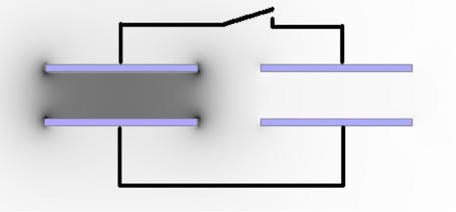
9. Ein Experiment mit zwei baugleichen Kondensatoren: Der eine wird geladen und dann vom Netzgerät getrennt. Dann wird der Schalter geschlossen.
(a) Was passiert mit der Ladung?
(b) Was kannst du über die Energie sagen, die ursprünglich im Feld des linken Kondensators steckte?
Die Energie im Feld der Kondensatoren hat auf die Hälfte abgenommen. Die fehlende Energie wurde zur Entropieerzeugung in den Leitungen verbraucht.
10. Das Bild wurde mit Fieldlab erzeugt. Es zeigt die Felder zwischen zwei baugleichen Plattenkondensatoren. Es sind einige Druckflächen (die grünen Linien sind ihre Schnitte mit der Bildebene) dargestellt. Was lässt sich über die Spannungen zwischen den Platten der beiden Kondensatoren sagen? Begründung.
Lösung:
Die ‚Linien‘ (Druckflächen) gleichen Potenzials haben im Feld des rechten Kondensators ungefähr den doppelten Abstand von dem im linken. Daher ist die elektrische Feldstärke im linken Kondensator doppelt so groß wie die im rechten. Da der Plattenabstand in beiden Kondensatoren gleich ist, ist die Spannung zwischen den Platten des linken Kondensators doppelt so groß wie die Spannung zwischen den Platten des rechten.
11. Das elektrische Feld außerhalb einer kugelförmigen geladenen Kugel nennt man Coulombfeld. Seine elektrische Feldstärke nimmt quadratisch mit dem Abstand vom Mittelpunkt der Kugel ab:
Was lässt sich über die Energiedichte in diesem Feld sagen?
Lösung:
Da die Feldstärke mit dem Quadrat des Abstandes abnimmt, nimmt die Energiedichte mit der 4-ten Potenz des Abstandes ab.
12. Die Ionosphäre (beginnt in einer Höhe von etwa 100 km Höhe) ist positiv elektrisch geladen, die Erdoberfläche negativ. Ionosphäre und Erdoberfläche bilden also eine Art Kondensator. Dieser entlädt sich langsam über die Luft (deren Leitfähigkeit nicht null ist): Es fließt der so genannte Schönwetterstrom von insgesamt etwa 1500 A. (Der Kondensator wird durch die ständig irgendwo stattfindenden Gewitter aufgeladen; insgesamt entlädt er sich also gar nicht.)
Berechne näherungsweise die mittlere Stromdichte des Schönwetterstroms. (Falls du Daten brauchst, die in der Aufgabenstellung nicht angegeben sind, schätze sie ab.)
13. Vergleiche die Energien, die man in einem Kondensator einerseits und in einem Akku derselben Größe andererseits speichern kann.
Hilfe:
Eine Mignonzelle hat eine Spannung von 1,5 V und liefert 0,8 Ah (d.h. sie kann 0,8 Stunden lang einen elektrischen Strom von 1 A liefern.)
Ein etwa gleich großer Kondensator hat eine Kapazität von 20 mF und verträgt eine Spannung
von 6 V.
14. Wir betrachten einen geladenen Kondensator: Plattenabstand 1cm, Plattenfläche 50 cm x 50 cm, elektrische Ladung 0,1 μC.
Berechne: Kapazität, elektrische Spannung, elektrische Feldstärke, Energiedichte, Gesamtenergie des Feldes.
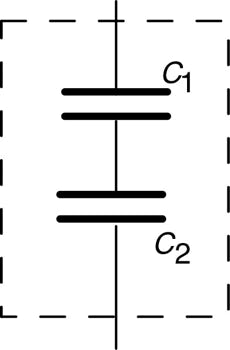
Nun wird eine 0,5 cm dicke Metallplatte M in die Mitte zwischen die Kondensatorplatten geschoben, siehe Abbildung; M hat denselben Flächeninhalt wie die Kondensatorplatten.
Hilfe: Du kannst dir vorstellen, dass aus dem einen Kondensator zwei neue entstanden sind.
Berechne die Kapazität der beiden Einzelkondensatoren.
Wie ist die Spannung zwischen M und P1, und zwischen M und P2?
Wie ist die Feldstärke innerhalb der eingeschobenen Platte?
Wie ist die Spannung zwischen P1 und P2?
Wie ist die Feldstärke zwischen M und P1, und zwischen M und P2?
Wie ist nach dem Hineinschieben von M die gesamte Feldenergie? Vergleiche mit vorher: Hat die Energie zu- oder abgenommen? (D.h. braucht man, um die Platte hineinzuschieben Energie, oder bekommt man welche?
15. Zwischen zwei parallelen, gleich großen Metallplatten – Länge 5 cm, Breite 3 cm, Abstand 4 mm – liegt eine elektrische Spannung von 50 V. Die Platten bilden eine Art Kondensator. Zwischen ihnen fliegt ein Proton in Längsrichtung hindurch. Beim Eintritt in das Gebiet zwischen den Platten ist der Impulsvektor des Protons parallel zu den Platten und es hat eine Geschwindigkeit von 2 000 000 m/s. Die Masse des Protons beträgt 1,67 · 10-27 kg.
Welchen Impuls hat das Proton beim Eintritt in den Bereich zwischen den Platten?
Wie groß ist der Impulsstrom, der zwischen den Platten in das Proton fließt?
Wie viel Impuls hat das Proton auf diese Art bekommen, wenn es aus dem Bereich zwischen den Platten wieder austritt?
Um welchen Winkel ist die Bahn des Protons am Ende geneigt?
Wie groß ist der Impulsstrom von der einen zur anderen Platte? Muss man bei der Berechnung den Beitrag des Protons zum Feld berücksichtigen?
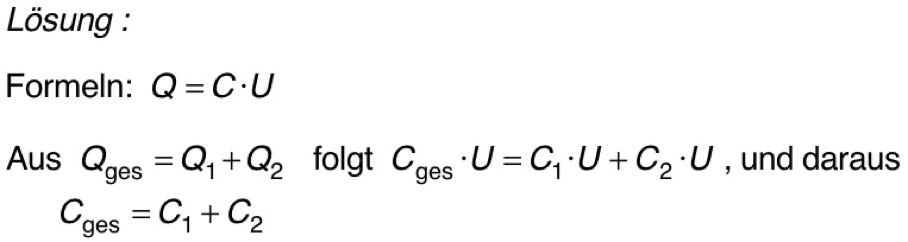
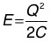

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Aliquam tincidunt lorem enim, eget fringilla